Practical Theory for Trapped Ion Experiments
01 October 2015
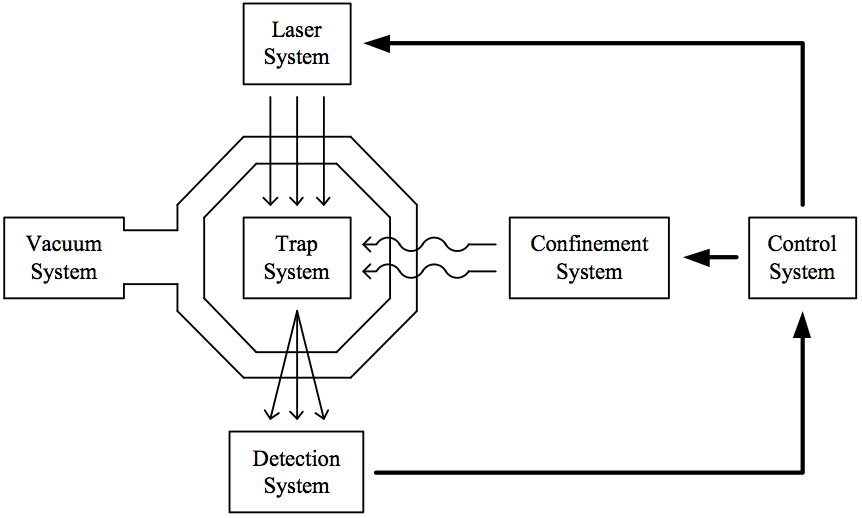
- Trap System: 4-rod Paul trap with atom ovens
- Vaccum System: keep <$10^{-11}$ torr UHV to reduce the background collision rate to <1/hour
- Confine System: RF helical resonator and DC voltage board
- Detection System: PMT and CCD to detect the fluorescence of ions
- Laser System
- FP cavity and Iodine cell to stabilize diode laser frequency
- EOM to generate sidebands
- AOM to shift center frequency and act as an optical switch
- Control System
- coherent quantum control with microwave horn and pulse laser Raman beams
- programmable TTL sequencer and waveform generators
Trap System
For atomic ions, $\Omega/2\pi>100$ kHz and $|V_0|<1000$ V, near the axis of the trap
\[\begin{aligned} \Phi(x,y,z,t)=&U_0\frac{1}{2}(\alpha x^2+\beta y^2+\gamma z^2)\\ &+V_0\frac{1}{2}(\alpha ' x^2+\beta ' y^2+\gamma ' z^2)\cos(\Omega t)\\ \end{aligned}\]where Laplace condition $\Delta\Phi=0$ implies
\[\begin{aligned} &\alpha+\beta+\gamma=0\\ &\alpha'+\beta'+\gamma'=0 \end{aligned}\]in Paul trap case
\[\begin{aligned} &-(\alpha+\beta)=\gamma>0\\ &\alpha'+\beta'=0 \end{aligned}\]and
\[\begin{aligned} \mathbf{E}(x,y,z,t)=\frac{\partial\Phi}{\partial\mathbf{u}}=&-\frac{\lambda U_ 0}{ {Z_ 0}^2}(2z\hat{z}-x\hat{x}-y\hat{y})\\ &-V_0\frac{x\hat{x}-y\hat{y}}{R^2}\cos(\Omega t) \end{aligned}\]
- time averaging of the AC field can be represented as a pseudopotential
- for single ion experiment, the small AC field along the z axis can be emitted
- there could be additional terms caused by
- imperfect geometry configuration
- addtional external field
- phase difference between AC electrodes
- use CPO3D to simulate and verify all these electric fields
For single ion of mass m and charge Q, from
\[m\ddot{u_ i}=QE_ i, i=x,y,z\]we get Mathieu equations
\[\ddot{u_ i}+(a_ i+2q_ i\cos(\Omega t))\frac{\Omega^2}{4}u_ i=0\]where
\[a_ x=a_ y=-\frac{1}{2}a_ z=-\frac{4Q\lambda U_ 0}{m{Z_ 0}^2\Omega^2}\]and
\[q_ x=-q_ y=\frac{2QV_ 0}{mR^2\Omega^2},q_ z=0\]when $|a_ i|,|q_ i|\ll 1$, set $\beta_ i=\sqrt{a_ i+q_ i^2/2}$, the first-order solution
\[u_ i(t)\approx A_ i\cos(\beta_ i \frac{\Omega}{2} t+\phi_ i)(1+\frac{q_i}{2}\cos(\Omega t))\]the main secular motion of the ion is harmonic oscillation, fast oscillation with frequency $\Omega$ is called ‘‘micromotion’’.
'’excess’’ micromotion caused by additional terms can be detected with TDC or Raman beams and then compensated with bias DC rods
The metal powder is heated and gasified from atom oven. A beam of Yb atoms is shooted into trap center, then ionized by a pair of strong 399nm and 370nm laser beams. Once the ion is Doppler cooled to limit
\[T_ D\approx\frac{\hbar\gamma}{2k_ B}\approx470\ \mu K\]where $\gamma=2\pi\cdot 19.7$ MHz is the linewidth of the cooling transition for $^{171}\mathrm{Yb}^+$ case, its internal electric levels plus external trap oscillator can be written as
\[\hat{H}^{(e)}+\hat{H}^{(m)}=\frac{\hbar\omega_ 0}{2}\sigma_ z+\hbar\omega_1 a^\dagger a\]and the diople coupling hamiltonian
\[\begin{aligned} \hat{H}^{(i)}&=-\mathbf{q}\cdot\mathbf{E}\ \mathrm{or}\ -\mathbf{\mu}\cdot\mathbf{B}\\ &=\hbar\Omega(\hat{\sigma}_ ++\hat{\sigma}_-)\cos(k\hat{x}-\nu t+\phi)\\ &=\frac{\hbar}{2}\Omega(\hat{\sigma}_ ++\hat{\sigma}_-)e^{\imath(\eta(\hat{a}+\hat{a}^\dagger)-\nu t+\phi)}+h.c. \end{aligned}\]if we apply an external wave field from either microwave horn or laser beam. Take interaction picture with respect to wave frequency
\[\hat{H}_ 0=\hat{H}^{(e)}+\hat{H}^{(m)}+\frac{\hbar\delta}{2}\sigma_ z\]where detuning $\delta=\nu-\omega_ 0-(m-n)\omega_1$, and apply rotating-wave approximation
\[\begin{aligned} \hat{H}_ I&=e^{\imath\hat{H}_ 0 t/\hbar}(\hat{H}^{(i)}-\frac{\hbar\delta}{2}\sigma_ z)e^{-\imath\hat{H}_0 t/\hbar}\\ &\approx\frac{\hbar\Omega}{2}(\hat{\sigma}_ +\exp(\imath(\eta(a e^{-\imath\omega_ 1 t}+a^\dagger e^{\imath \omega_ 1 t})-(m-n)\omega_ 1 t-\phi))+h.c.)-\frac{\hbar\delta}{2}\sigma_z \end{aligned}\]The coupling term
\[\begin{aligned} \langle\uparrow,m|\hat{H}_I|\downarrow,n\rangle&=\langle\uparrow,m|e^{\imath\hat{H}_ 0 t/\hbar}(\hat{H}^{(i)}-\frac{\hbar\delta}{2}\sigma_ z)e^{-\imath\hat{H}_0 t/\hbar}|\downarrow,n\rangle\\ &=e^{\imath(1/2(\omega_0+\delta)+m\omega_1+1/2(\omega_0+\delta)-n\omega_1) t}\langle\uparrow,m|\hat{H}^{(i)}-\frac{\hbar\delta}{2}\sigma_z|\downarrow,n\rangle\\ &=e^{\imath\nu t}\langle\uparrow,m|\frac{\hbar}{2}\Omega(\hat{\sigma}_ ++\hat{\sigma}_-)e^{\imath(\eta(\hat{a}+\hat{a}^\dagger)-\nu t+\phi)}+h.c.|\downarrow,n\rangle\\ &=\frac{\hbar\Omega}2\langle m|e^{\imath(\eta(\hat{a}+\hat{a}^\dagger)+\phi)}+e^{\imath(-\eta(\hat{a}+\hat{a}^\dagger)+2\nu t-\phi)}|\downarrow,n\rangle\\ &\approx\frac{\hbar\Omega}{2}e^{\imath\phi}\langle m|e^{\imath\eta a^\dagger+\imath\eta a}|n\rangle\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} \langle m|e^{i\eta a^\dagger} e^{i\eta a}|n\rangle\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} (\sum_ {j=0}^\infty\frac{(\imath\eta)^j}{j!}(a^\dagger)^j\langle m|)\cdot(\sum_{j=0}^\infty\frac{(\imath\eta)^j}{j!}a^j|n\rangle)\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} (\sum_ {j=0}^m\frac{(\imath\eta)^j}{j!}\sqrt{\frac{m!}{(m-j)!}}\langle m-j|)\cdot(\sum_{j=0}^n\frac{(\imath\eta)^j}{j!}\sqrt{\frac{n!}{(n-j)!}}|n-j\rangle)\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} (\sum_ {k=0}^m\frac{(\imath\eta)^{m-k}}{(m-k)!}\sqrt{\frac{m!}{k!}}\langle k|)\cdot(\sum_{k=0}^n\frac{(\imath\eta)^{n-k}}{(n-k)!}\sqrt{\frac{n!}{k!}}|k\rangle)\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} \sum_ {k=0}^{n_ <}\frac{(\imath\eta)^{m+n-2k}\sqrt{m!n!}}{(m-k)!(n-k)!k!}\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi}(\imath\eta)^{n_ >-n_ <}\sqrt{\frac{n_ < !}{n_ >!}} \sum_ {k=0}^{n_ <}\frac{(\imath\eta)^{2(n_ <-k)}}{(n_ <-k)!}\frac{n_ >!}{(n_ >-k)!k!}\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi}(\imath\eta)^{n_ >-n_ <}\sqrt{\frac{n_ < !}{n_ >!}} \sum_ {k=0}^{n_ <}(-1)^{n_ <-k}\binom{n_ >}{k}\frac{(\eta^2)^{n_ <-k}}{(n_ <-k)!}\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi}(\imath\eta)^{|m-n|}\sqrt{\frac{n_ < !}{n_ >!}} \sum_ {j=0}^{n_ <}(-1)^j\binom{n_ <+|m-n|}{n_ <-j}\frac{(\eta^2)^j}{j!}\\ &=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} (i\eta)^{|m-n|}\sqrt{\frac{n_ < !}{n_ >!}}L_ {n<}^{|m-n|}(\eta^2)\\ & \approx \frac{\hbar\Omega}2 e^{-\frac{\eta^2}2+i\phi} (i\eta)^{|m-n|}\sqrt{\frac{n_ < !}{n_ >!}}(\binom{n_ >}{n_ <}-\binom{n_ >}{n_ <-1}\eta^2) \end{aligned}\]where Laguerre polynomial
\[L_ n^\alpha(x)=\sum_ {j=0}^n(-1)^j\binom{n+\alpha}{n-j}\frac{x^j}{j!}=\binom{n+\alpha}{n}-\binom{n+\alpha}{n-1}x+\cdots\]Specially, for carrier transition $ |\downarrow,n\rangle\rightarrow |\uparrow,n\rangle$
\[\hat{H}_I=\frac{\hbar\Omega}2 e^{-\frac{\eta^2}2}\left( \sigma_+e^{-i\varphi}+h.c \right) -\frac{\hbar\delta}2\sigma_z\]For blue sideband $ |\downarrow,n-1\rangle\rightarrow |\uparrow,n\rangle$, and red sideband $ |\downarrow,n\rangle\rightarrow |\uparrow,n-1\rangle$
\[\hat{H}_I =\frac{\sqrt n\hbar\Omega}2 \eta e^{-\frac{\eta^2}2}\left[ \sigma_+ e^{-i(\varphi-\frac\pi2)} +h.c \right] -\frac{\hbar\delta}2\sigma_z\]Open Problems
two ions are not stable in high trap z direction rf from dc rods 崔凯枫 from Wuhan: protection sequence doesn’t work
