Experimental Progress on Quantum Computing with Atomic Qubits (Part 1)


26 January 2018
张翔
中国人民大学物理系 离子量子科学实验室
2018.01.26
Why
经典计算面临的困难
- 日益增长的计算需求
- 民用(大数据/人工智能/物联网/区块链)
- 工业(天气预报/化学/制药)
- 科研(凝聚态/材料/蛋白质)
- 算法困难
- NP难问题
- 复杂系统模拟
- 物理困难
- 有限光速要求提高集成密度
- 受限于量子隧穿(摩尔定律失效)
- 以及发热密度(不可逆计算信息熵)
摩尔定律发展趋势
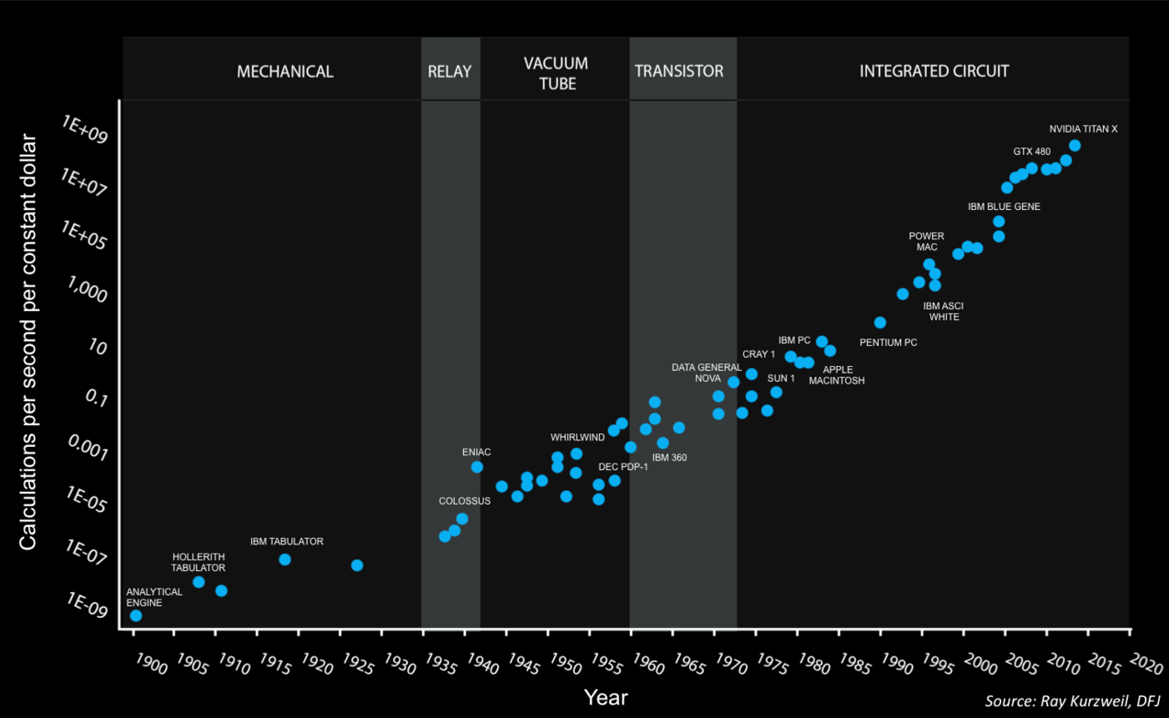
量子计算的发展
- 1982年由物理学家Feynman提出
- 可控量子系统模拟其他量子力学系统
- 解决指数复杂度的量子体系模拟问题
- 随着几个复杂度优于经典算法的量子算法被发现
- 量子计算渐渐成为研究热点
- 加速Google搜索排名的解线性方程组量子算法
- 人工智能相关的量子机器学习算法
- Quantum Algorithm Zoo
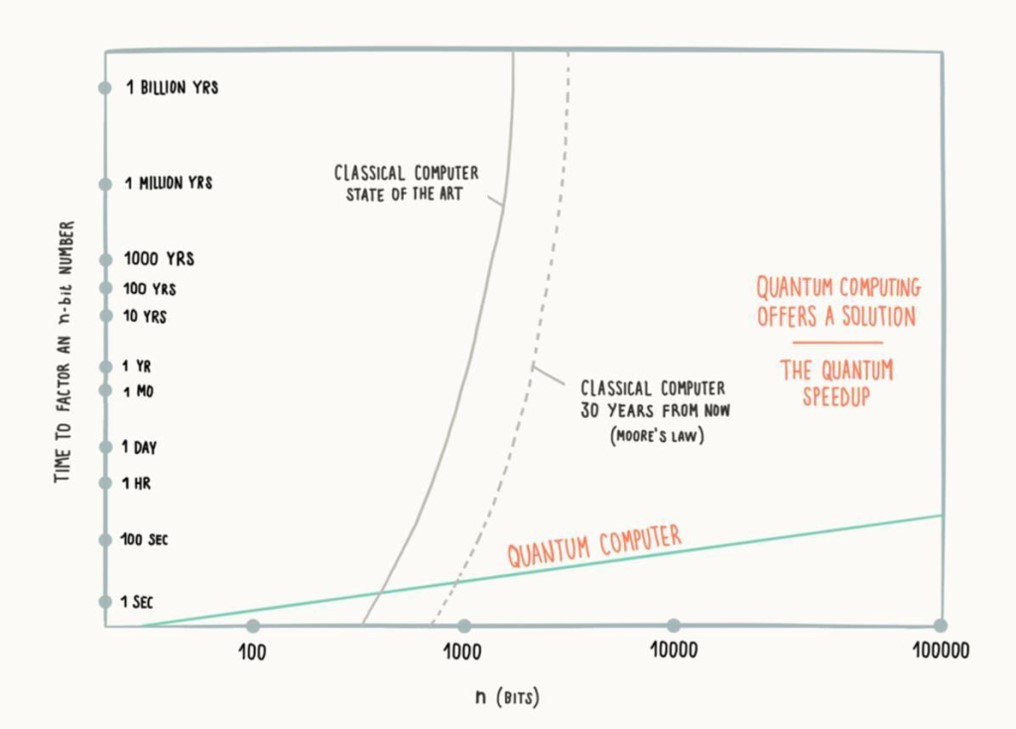
Shor算法分解速度
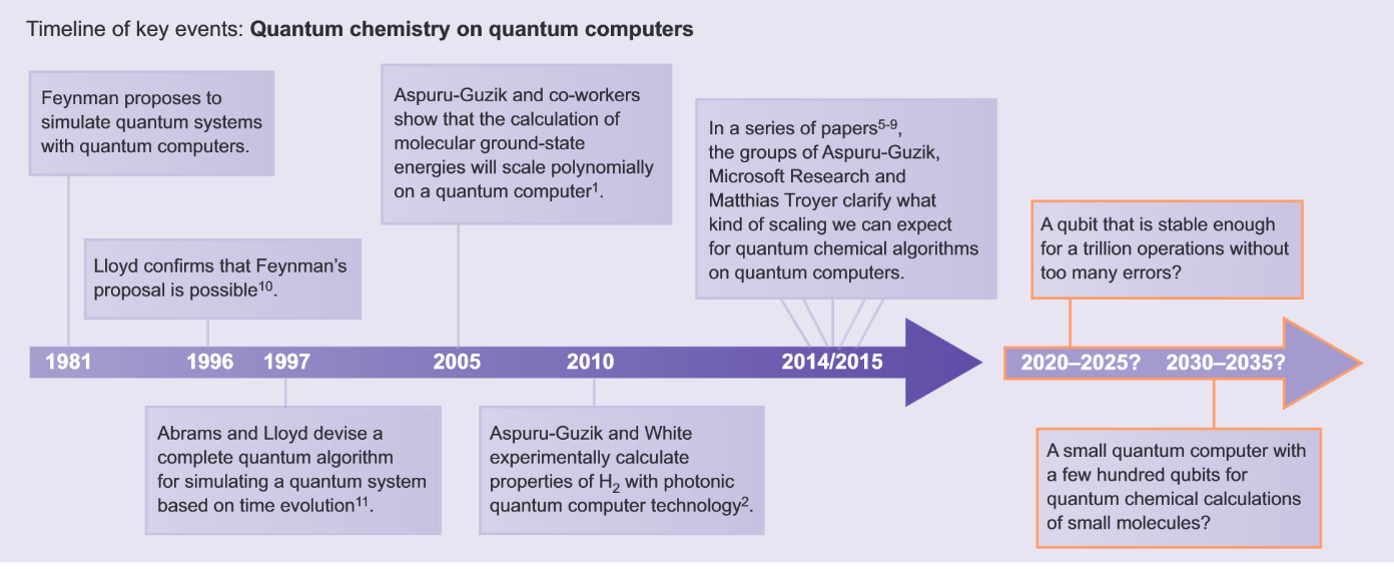
Nat. Chem. 7, 361–363 (2015)
What
Quantum v.s. Classical
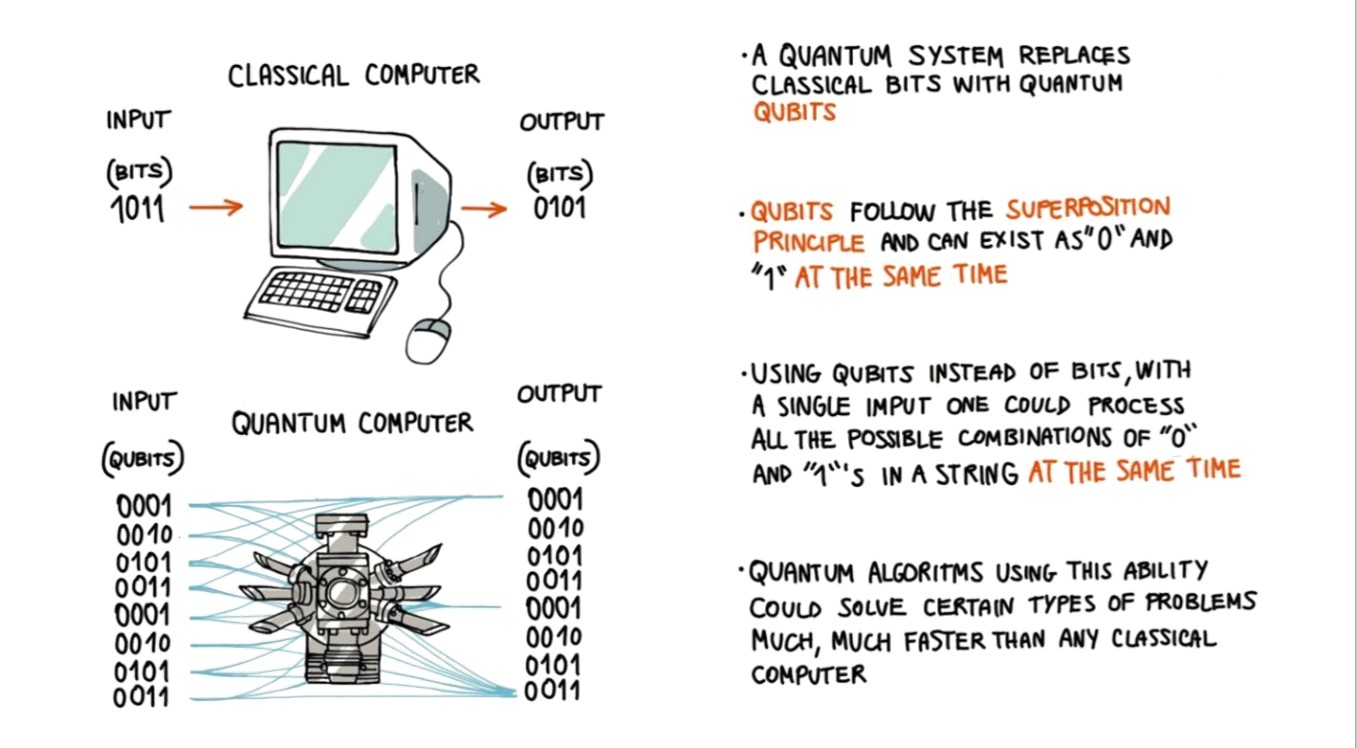
量子门电路(代数模型)
- 量子态
- 量子比特:2维复空间(二能级系统)
- 量子寄存器:多量子比特态空间直积
- 量子测量:密度矩阵求偏迹
- 量子门
- 可组合实现所有量子计算的通用量子门组
- 可组合实现所有经典计算的Toffoli量子门
- 量子编程
量子态记号1
本征态内积$\langle 0|0\rangle=\langle 1|1\rangle=1, \langle 0|1\rangle=0$
| 量子态 | 复向量 | \(\lvert\psi_0\rangle=\frac{1}{\sqrt{2}}\left(\lvert 0\rangle+i\lvert 1 \rangle\right)=\frac{1}{\sqrt{2}}\left(\begin{matrix}1 \\\\ i\end{matrix}\right)\) |
| 测量概率 | 系数模方 | \(P(\lvert 0\rangle)=P(\lvert 1\rangle)=\frac{1}{2}\) |
| 量子门 | 复矩阵 | \(\hat{U}=\frac{1}{\sqrt{2}}\left(\begin{matrix}1 & -i\\\\ i & -1\end{matrix}\right)\) |
| 态操作 | 矩阵乘 | \(\lvert\psi_1\rangle=\hat{U}\cdot\lvert\psi_0\rangle=\left(\begin{matrix}1 \\\\ 0\end{matrix}\right)=\lvert 0 \rangle\) |
量子寄存器
- 3比特(未归一化)直积态表示为Kronecker积1$(\lvert 0\rangle-\lvert 1\rangle)\otimes \lvert 0\rangle \otimes(\lvert 0\rangle+\lvert 1\rangle)$=$\left(\begin{matrix}1 \\ -1\end{matrix}\right)\otimes \left(\begin{matrix}1 \\ 0\end{matrix}\right)\otimes \left(\begin{matrix}1 \\ 1\end{matrix}\right)$
- $\lvert 000\rangle +\lvert 001\rangle-\lvert 100\rangle-\lvert 101\rangle=(1,1,0,0,-1,-1,0,0)’$
- 纠缠态$\lvert 000\rangle+\lvert 111\rangle=(1,0,0,0,0,0,0,1)’=\lvert 0\rangle+\lvert 7\rangle$
- 部分量子测量2相当于密度矩阵$\rho=\lvert\psi\rangle\langle\psi\rvert$求偏迹3
量子门1
- 量子门U为酉阵2:\(\langle \psi_1\mid \psi_1\rangle=\langle \psi_0\mid U^\dagger U\mid \psi_0\rangle=1\Rightarrow U^\dagger U=I\)
- 存在自共轭(Hermite3)矩阵H使得$U=e^{iH}$
- 哈密顿量(Hamiltonian4)不含时的Schrödinger方程5${\hat {H}}|\psi (t)\rangle =i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle$的解为\(\lvert\psi(t)\rangle=\hat{U}(t)\lvert\psi(0) \rangle,\hat{U}(t)=e^{-i\hat{H}t/\hbar}\)
- 一般分解为基本操作(通用量子门6 7)序列\(U\approxeq U_n\cdots U_1=e^{-i H_n t_n/\hbar}\cdots e^{-i H_1 t_1/\hbar}\)
- 部分操作通过有效哈密顿量8或绝热演化9实现
How
DiVincenzo判据1
IBM科学家DiVincenzo提出量子计算机物理实现标准
- 系统必须能够包含充分多、准确定义的量子比特
- 系统必须能够将所有量子比特准确地初始化到一个简单的初态
- 系统中的量子比特保持相干性的时间要足够长,应当远长于量子门操作的时间
- 在系统中应当能实现一组“通用量子门”,即通过这些门的排列组合,可以逼近任何一个量子门
- 可以准确的测量任何一个量子比特,被测量后即被准确的投影到可观测量的一个本征态,而其它未被测量的量子比特则不受影响
物理实现
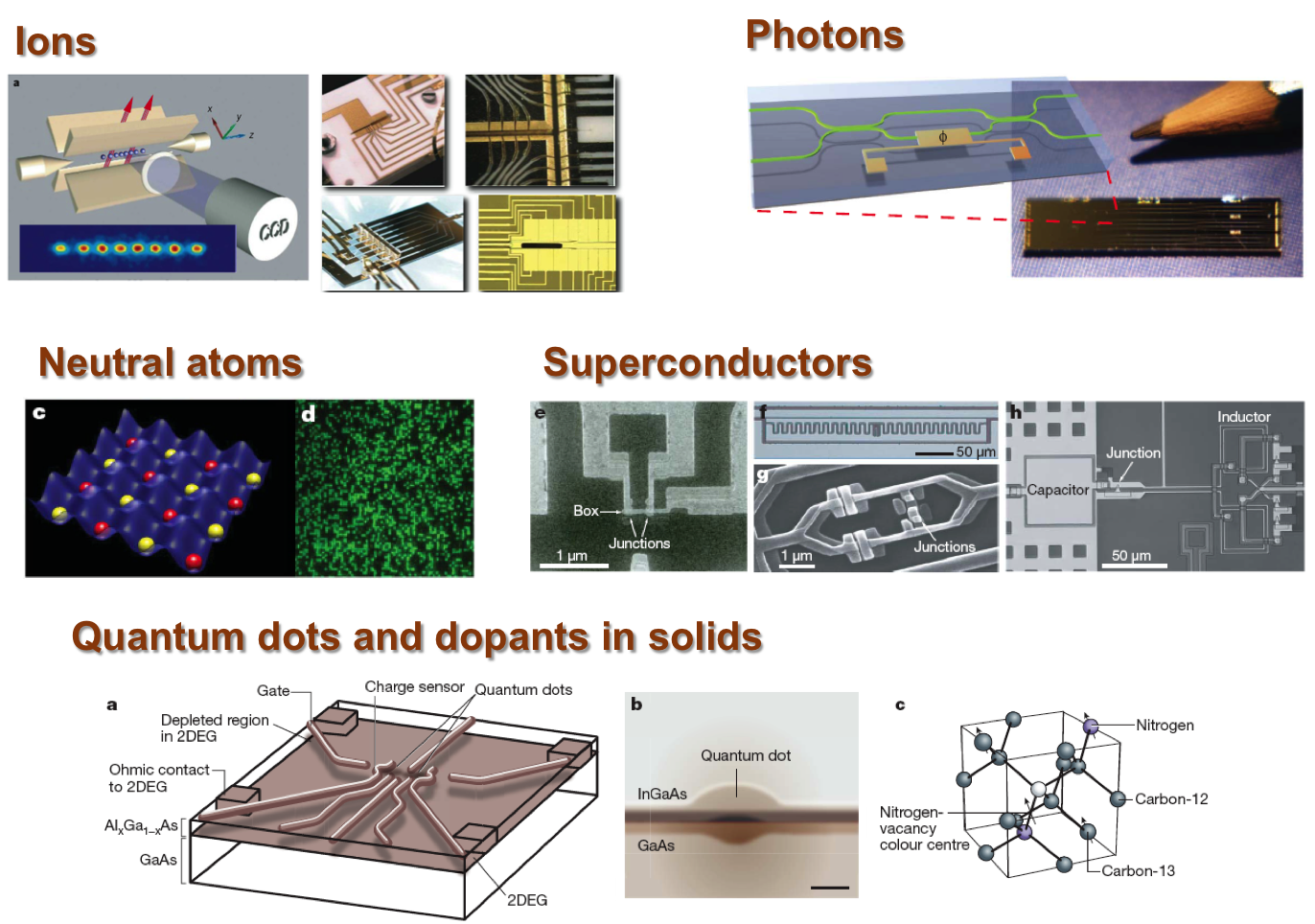
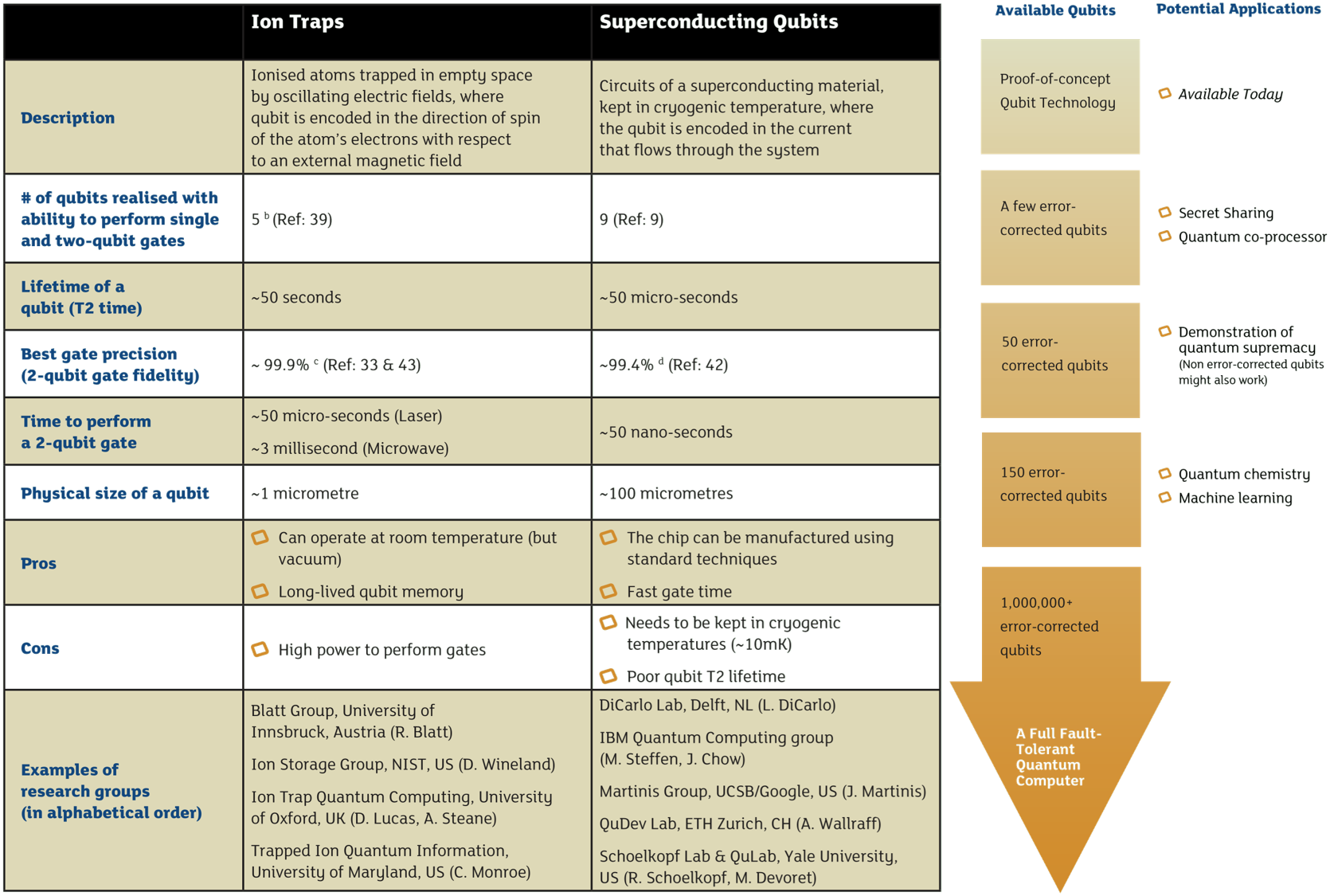
主流实现对比及应用场景
耦合与量子门实现
- 量子门实现取决于耦合类型,以电偶极跃迁为例 \(\hat{H}=-q\hat{\overrightarrow{r}}\cdot \overrightarrow{E}=-q(E_x\hat{x}+E_y\hat{y}+E_z\hat{z})\)
- $\hat{H}$本征态$\mid\psi\rangle$具有确定的宇称,因此$\langle\psi\mid\hat{x}\mid\psi\rangle=0$
- $\hat{H}$对角元为0,在二能级系统中可表示为 \(\hat{H}=\left(\begin{matrix}0 & \hbar\Omega^* \\\\ \hbar\Omega & 0\end{matrix}\right)\rightarrow \hbar\lvert \Omega \rvert\left(\begin{matrix}0 & 1 \\\\ 1 & 0\end{matrix}\right), \lvert \Omega \rvert \propto \lvert E \rvert\)
- $\hat{H}^{(e)}=\frac{1}{2}\hbar\Omega e^{i (\nu t+\phi-\overrightarrow{k}\cdot \hat{\overrightarrow{r}})}\hat{\sigma}_x+h.c.$含自旋及空间耦合
- 控制幅度频率相位分段函数实现各种量子门演化
实验序列分解(单比特)
Pauli矩阵1$\sigma_x=\left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right),\sigma_y=\left(\begin{matrix}0 & -i \\ i & 0\end{matrix}\right),\sigma_z=\left(\begin{matrix}1 & 0 \\ 0 & -1\end{matrix}\right)$
- 一般形式的2阶酉阵2 \(U=e^{i\phi}\left(\begin{matrix}e^{i\phi_1}\cos{\theta} & e^{i\phi_2}\sin{\theta} \\\\ -e^{-i\phi_2}\sin{\theta} & e^{-i\phi_1}\cos{\theta}\end{matrix}\right)\)
- 设$\phi_1=\delta_1+\delta_2,\phi_2=\delta_1-\delta_2$则 \(\begin{align}U &= e^{i\phi}\left(\begin{matrix}e^{i\delta_1} & 0 \\\\ 0 & e^{-i\delta_1}\end{matrix}\right)\left(\begin{matrix}\cos{\theta} & \sin{\theta} \\\\ -\sin{\theta} & \cos{\theta}\end{matrix}\right)\left(\begin{matrix}e^{i\delta_2} & 0 \\\\ 0 & e^{-i\delta_2}\end{matrix}\right) \\\\ &= e^{i\phi}e^{i \sigma_z \delta_1}e^{i \sigma_y \theta}e^{i \sigma_z \delta_2}\end{align}\)
容错量子计算
- 错误来源
- 退相干(环境影响)
- 量子操控误差(有限参数精度)
- 量子态不可克隆,需要特殊的纠错方案
- 量子纠错编码(如Surface Code)
- 无退相干子空间
- 几何量子计算
- 拓扑量子计算
可能需要上万个物理qubit实现一个逻辑qubit
认识误区
- N比特=N比特纠缠=N比特量子计算机
- 超导量子计算使用高温超导材料就不需要低温
- 仍然需要降到mK,保证环境热噪声远小于GHz能级差
- 量子计算其实是某种并行计算(比如类似于GPU计算)取了个好听的名字
- 希望今天后不再会误解
我们能做什么
- 物理问题/数学问题/技术问题
- 新材料/Majorana费米子/拓扑量子计算
- 理论:量子纠错/动态解耦合/最优实验控制序列
- 设备:窄线宽激光器/任意波形发生器/制冷机
- 技术:微纳加工/激光稳频/控制系统
进阶阅读
Shor算法
初等数论记号
- a整除N记作$a\mid N\Leftrightarrow N=k\cdot a, k\in \mathbb{Z}$
- a同余于b模N记作$a\equiv b\pmod N\Leftrightarrow a-b\mid N$
- a与b的最大公约数记作$\gcd(a,b)$(辗转相除法1)
RSA公钥系统1
Alice随机产生大质数$p,q$,$N=p\cdot q$
- 公开发布公钥$(N,e)$。$e<r=\phi(N)=(p-1)(q-1)$
- 自己保存私钥$(N,d)$。$e\cdot d\equiv 1\pmod r$
- Bob发送消息$m$,使用公钥加密为$c\equiv m^e\pmod N$
- Alice收到密文$c$,根据Euler定理2使用私钥解密$c^d\equiv m^{e\cdot d}=m^{1+k\cdot r}=m(m^r)^k\equiv m\pmod N$
RSA例子1
$p=11,q=13,e=23,m=69$(‘E’)
大数分解
破解私钥d需要对N进行整数分解
位数$n=\log(N)$,分解算法的时间复杂度
- 试除法:$\sqrt{N}=e^{n/2}$
- 普通数域筛选法(GNFS)1:$O(e^{(\frac{64}{9}n)^{1/3}\log^{2/3}{n}})$
- Shor算法2,3:$O(n^3)$
台式机破解RSA-2048需要$6.4\times 10^{15}$年4
模阶方法
- 随机取$a<N$,若$\gcd(a,N)\neq 1$,则$\gcd(a,N)$是N的非平凡因子
- 否则求a的阶r,即$f(x)=a^x\pmod N$的周期。应有$a^r\equiv 1\pmod N$
- 若r为奇数,或$a^{r/2}\equiv -1\pmod N$,返回第一步
- 因为$N|a^r-1=(a^{r/2}-1)(a^{r/2}+1)$,$N\nmid a^{r/2}\pm 1$,所以$\gcd(a^{r/2}\pm 1,N)$都是N的非平凡因子
模阶方法例子1
\(N=143,a=2,r=60\rightarrow 143=11\times 13\)
量子Fourier变换
两个q量子比特寄存器,$N^2\le Q=2^q< 2N^2$,初态:$|(0\cdots 0)_q\rangle\otimes|(0\cdots 0)_q\rangle$
- 并行的q个Hadamard门作用于寄存器1:$Q^{-1/2}\sum_{k=(0\cdots 0)_q}^{(1\cdots 1)_q}\lvert k\rangle\otimes\lvert 0=(0\cdots 0)_q\rangle$
- 模幂门$f(\lvert k\rangle\otimes\lvert 0\rangle)=\lvert k\rangle\otimes\lvert a^k\pmod N\rangle$作用于寄存器1,2:$Q^{-1/2}\sum_{k=0}^{Q-1}\lvert k\rangle\otimes\lvert a^k\pmod N\rangle$
- 测量寄存器2,不妨设其坍缩到$\lvert m\rangle$态:$Q^{-1/2}\sum_{k\in A_m=\lbrace k\lvert a^k\equiv m\pmod N\rbrace}\lvert k\rangle\otimes\lvert m\rangle$
- 设$\omega$为Q次原根,量子Fourier变换作用于寄存器1:$Q^{-1}\sum_{k\in A_m}\sum_{n=0}^{Q-1}\omega^{kn}\lvert n\rangle\otimes\lvert m\rangle$
相位估计
- 测量寄存器1,不妨设测量到$\lvert n\rangle$态,测量概率$P_n=\lvert Q^{-1}\sum_{k\in A_m}\omega^{nk}\rvert^2$
设a的模阶为$r$,则$A_m=\lbrace k_m+br|0\le b\le b_m=\lfloor(Q-1-k_m)/r\rfloor\rbrace$,$P_n=Q^{-2}\lvert\sum_be^{\frac{2\pi i}{Q}n(k_m+br)}\rvert^2=Q^{-2}\lvert\sum_be^{b\frac{nr}{Q}2\pi i}\rvert^2$
-
设$t=\frac{nr}{Q}$,若t为整数,则$P_n=Q^{-2}(b_m+1)^2$
-
否则$P_n=\frac{\sin^2{(b_m+1)\pi t}}{Q^2\sin^2{\pi t}}$,$t$越接近整数,$P_n$越大
-
设$c$是最接近$t=\frac{nr}{Q}$整数,则$\frac{c}{r}$是$\frac{n}{Q}$的有理数近似
连分式展开
-
例如$0.234375=\frac{15}{64}=\frac{1}{4+\frac{4}{15}}=\frac{1}{4+\frac{1}{3+\frac{3}{4}}}=\frac{1}{4+\frac{1}{3+\frac{1}{1+\frac{1}{3}}}}$
-
各级连分数$[4]=\frac{1}{4}=0.25$,$[4,3]=\frac{1}{4+\frac{1}{3}}=\frac{3}{13}\approx 0.231$,$[4,3,1]=\frac{1}{4+\frac{1}{3+\frac{1}{1}}}=\frac{4}{17}\approx 0.235$,均为$\frac{15}{64}$的有理数近似
若$\frac{d}{s}$是$\frac{n}{Q}$的有理数近似,且满足$s<N,\lvert\frac{d}{s}-\frac{n}{Q}\rvert<\frac{1}{2Q}$,则有很大概率$s=r$或$s|r$
Shor算法例子1
\(N=35,a=2\rightarrow 35=5\times 7\)
